This also involves working from the lefthand side to the righthand side of the abacus, involving the use of a slightly different substution method. We outline it below.
Numbers less than 10 do not require the substitution method since they can be handled on the rod itself. So 9 - 6 would just meant that a topbead and a unitbead would be removed from the abacus representation of 9, leaving three unitbeads.
When subtracting, it is usual to subtract the smaller number from the larger. Since there is no sign to represent negative numbers on an abacus, the operator will have to know if the the answer is negative or not by him/herself.

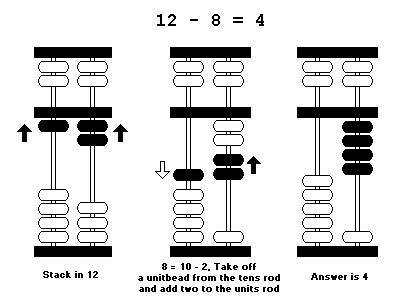
From our substitution method, we note that 8 = 10 - 2. If we place this into 12 - 8 we get,
12 - (10 - 2) = 12 - 10 + 2
This means, we take off a unitbead in the tens column, and add two unitbeads into the units column.
Try the following out:
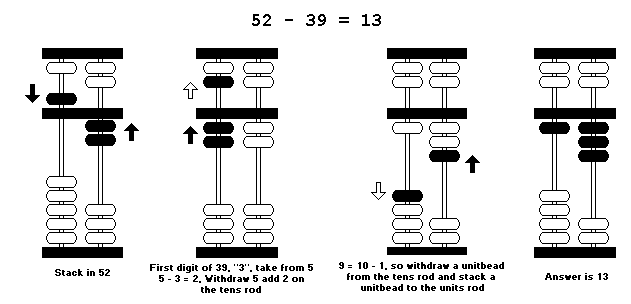
The above principle is applied to the above, but we take it a digit at a time, starting again from the left.
Try the following out:
Before, we asked you to add 123456789 successively to itself nine times to get 1111111101. It is now time to try subtracting 123456789 from 1111111101 successively. To help check your work, the numbers you should get at each stage is again given.
© Dylan W.H.S. 1996-onwards
You can e-mail me here on anything you like!
With thanks to Alex and Brian for correcting my arithmetical errors.